What Happens During My Tutoring Sessions?

I’ve been in a few situations in the past week which have got me thinking that people have preconceived (and inaccurate!) ideas of what happens during a tutoring session.  I want to offer some insights into what I do as a tutor.

My sessions are, as a rule, student-led.  As a tutor, I am here to meet my students’ needs, and I want their needs to guide our sessions.  That means I’m not following a script or a checklist.  I’m listening to my students, hearing their concerns, their confusions.  I’m finding them on the map of learning and meeting them there.

A tutoring strength of mine is flexibility.  Because I don’t have preconceived notions of what any given tutoring session should look or feel like, I feel very free to make each session unique.  That’s not to say that I feel compelled to reinvent the wheel, but I think there is enormous power in the collaboration between tutor and student.

Allow me to be give you some concrete examples of what can happen in my tutoring sessions.

* We can start from “I’m totally lost in this class.”  It’s not uncommon for students to tell me they are lost and frustrated with a class.  I have such love and admiration for their willingness to tell me how they are feeling.  That takes courage.  When a student is lost, we start a dialogue so I can find a starting point for our lessons.  From there, I can create entire customized lessons to help my student build a base of knowledge.  Generally, I think that simple is better in these situations.  Yes, science is large and complex, and I don’t mean to diminish that truth.  But we learn new ideas in bite-sized chunks, and I think it’s better for my student to walk away from a tutoring session with one new idea that they understand rather than five ideas that leave them confused and frustrated.

* Lessons can be improvised from homework, practice problems, or class notes.  Much of what I do is teaching mini-lessons that are centered around exam preparation.  Feedback from students on these tutoring sessions has been really positive, so I’m happy to keep going.  My students crave more than the right answers.  They genuinely want to understand the how and why of their subjects.  I strive to create interactive sessions so that my students are actively engaged as we work through the material.  Many students want to participate, and I’m happy to co-create our learning environment with them.

* Yes, sometimes we work through homework assignments together.  We do homework together.  Homework is the bread and butter of learning.  Again, my students are seeking an understanding, not just the right answers.  When we work through the homework, we’re having a conversation.  And if a mini-lesson is needed, then that’s what we do together.

* I share resources, advice, and exam strategies.  I’m aware that many students feel the pressure to get it all done, so time is of the essence.  

And now it’s your turn: have you ever worked with a tutor?  What was your experience like?  Would you work with a tutor again?

(And if you have any questions for me about my tutoring, feel free to ask them below in the comments!  Happy learning.)

LESSON: Heat Transfer, Part Two

If you’re new to this site, here is Part One of my lesson on heat transfer.  This lesson will be building on the ideas from Part One.

Now we’ve established that we can calculate values for heat transfer using the formula q = nC[DeltaT].  (Pretend that Delta is a triangle, please.)  Let’s work through a more difficult problem.  This one comes from Chemistry (Third Edition) by John Olsmsted III and Gregory M. Williams.

A silver coin weighing 27.4 g is heated to 100.0 degrees C in boiling water.  It is then dropped into 37.5 g of water initially at 20.5 degrees C.  Find the final temperature of water and coin.

Here is an example of a problem in which we cannot just look at the values given by the problem and perform a plug-and-play calculation.  We are going to use q = nC[DeltaT] but not before we do some algebra work.  Let’s consider the values we have on hand.

Do you see the dilemma?  We have two unknowns, which means we can’t simply plug and play to get an answer.

But notice that we have the same unknowns for the silver coin and water, so perhaps we can use the set of unknowns to set up an algebra equation with a single unknown.

In this problem, we start off with two different systems: the hot silver coin and the room temperature water.  When the coin is dropped into the water, it will transfer heat to the water until the new “system” (coin + water) are at equilibrium, which means SAME TEMPERATURE.  (Also, does “transfer heat” mean anything to you?  If you guessed q, as in heat flow, then you are correct and you get a gold star. )

To put this in mathematical terms:

-q_coin = +q_water   

All the heat that flows out of the coin will be heat that flows into the water.  Furthermore, if q = nC[deltaT], then:

-(nC[deltaT])_coin = (nC[deltaT])_water   

And now we’ve reduced our unknown to one term, final temperature T_f.

Here is the full-length solution, starting from the equation above.

And there you have it!  Now it’s your turn: using the same problem from above, what would the final temperature of water and coin be if the coin were made of pure copper?  The molar heat capacity of copper is 24.435 J/mol K.

(I’ll provide the answer if someone asks for it in the comments.)

More Drawing, More Learning

If you feel like you are living inside the pressure cooker of perfection, let me assure you :

You are not alone.

I have a hypothesis that collectively, we have become so good at the game of school and scholarly achievement that what used to be learning has been replaced by an unrelenting pressure to get straight A’s and achieve, achieve, achieve at all costs.  A sad price for this pressure is a loss of creativity and innovation.  But learning doesn’t happen without risk.  How can I encourage you to take some risks in your academic life?

I’ll start by offering a confession: I wish I were perfect, but I know I’m not.  To accept my less-than-perfect nature is a daily challenge.  For me, grace is found in the space where I can accept myself as I really am.  Grace is also found in that space where I am striving for something I want.  This is the paradox of ambition: it gives us a goal, something for which to strive, yet we don’t want to pin our self-worth on the achievement of that goal.  It’s okay to fail, and it’s okay to not want to fail.

This month, I’ve been reviewing thermodynamics at the general chemistry level, and I decided to make a “mind map” for myself.  A mind map is a a brainstorming diagram in which you connect ideas, write notes for yourself, even draw images if that’s your thing.  I had the idea that I would share my mind map on this site, but as I drew it, I started to think to myself, Oh, it’s not good enough to share.  It’s messy.  Other people will think it’s not pretty enough.

And then I realized the mind map had something to teach me, which is that learning is messy.  If I want my students to feel comfortable making mistakes, then maybe I should give myself the same grace.  Plus, mind maps are awesome!  They're great for studying.  To make a mind map, you have to actively engage with the material, which I find is better for studying and remembering the important ideas.

So here is my messy mind map for thermodynamics.  Feel free to use it for your own studying!  Or draw your own mind map to help you learn a new subject.  If you prefer to download it, I’ve included a link below for that too. 

{Rose-Anne’s Thermodynamics Mind Map. Click on the image to see a bigger version!}

Click to download the Thermodynamics Mind Map from Google Drive

Chemistry Lessons

This page is an index of all the general chemistry lessons I’ve published on this site. Enjoy and happy learning!

(Have any questions for me? Connect with me by e-mail at r-meissner@u.northwestern.edu or on Twitter. I’m @wormthoughts.)

* Heat Transfer: Part One

* Heat Transfer: Part Two 

* And to help you study: some study tips to do your best in general chemistry. 

Genetics Lessons

This page is an index of all the genetics lessons I’ve published on this site.  Enjoy and happy learning!

(Have any questions for me?  Connect with me by e-mail at r-meissner@u.northwestern.edu.)

* Conditional Probability

* Mitotic Recombination: Twin Spots

* Human Blood Type and Population Genetics

* Selection Pressure and Changing Allele Frequencies

* Selection Pressure, Part Two

Bonus: here are some great on-line resources for genetics.

* How radiation can damage DNA (the first graphic on this page is terrific)

* A good (and very technical) guide to types of DNA damage

LESSON: Heat Transfer, Part One

I wrote recently about the importance of algebra in general chemistry.  To illustrate, I’m going to present a lesson in two parts.  This first part is an example of what I call “plug and play” chemistry problems.

I’ve been brushing up on thermodynamics at the gen chem level.  Thermodynamics is a very math-driven branch of chemistry, so it’s a lot of equations and a little bit of theory.  There are at least two conceptual ways to approach problems:

1) Envision the process being described, determine the unknowns, then select the appropriate equation that describes (mathematically) the flow of energy in the system.

2)  Write down the values provides (such as heat capacity and initial temperature) and the value for which you have to solve (such as final temperature), find a formula that contains those terms, then solve for the unknown.

Option #1 is definitely the better choice and the one for which we should strive as we’re learning.  But if I’m honest, I think a lot of us are tempted to use #2 if we can get away with it.  In the second part of this lesson, I’ll show you an example of how option #2 can be insufficient.  Additionally, thermodynamics uses signs (+/-) to indicate the flow of energy into or out of a system.  Because of that, it’s a really good idea to get in the habit of imagining the process so you can double check your math and your signs.  (Or draw it out!  Drawing is always a good idea when studying science.)

(More on drawing later, I think.  It’s a topic worth exploring for science students.)

Let’s consider the following problem and how to find a solution.

You drop a pure copper penny on the ground while walking to breakfast one day.  The penny’s mass is 2.50 g.  At the time you lost it, the penny’s temperature was 20 degrees C.  When you find it later, the penny is 25 degrees C.  How much energy did the penny absorb from its surroundings between the time you lost it and the time you recovered it?

This problem is pretty simple, but let’s draw a diagram so we can visualize the energy flow.

Heat is flowing into the copper penny from the sun, thus raising the temperature of the copper.

Now let’s apply some technical labels to help us find the right formula.

A quick review of terms:

q = heat flow, usually measured in Joules (J).

T_i = initial temperature (can be degrees C or K)

T_f = final temperature (must have the same units as T_i)

What else do we need to know to solve this problem?  We need to know how easily copper absorbs heat from its surroundings.  This material property is known as heat capacity, and the heat capacity is different for different substances.  The molar heat capacity for copper at 25 degrees C is 24.435 J/mol K.  What does this value mean?  It means that 1 mole of copper requires 24.435 J to raise the temperature 1 K.

(For our purposes, we’ll assume that the heat capacity for copper is the same at 20 degrees C and 25 degrees C.)

Which formula expresses the thermodynamic question asked in this question?

Now that we have a formula to connect heat flow to the change in temperature in a specific substance, we can plug in the values from above and solve the problem.

(Note that in this problem, K and C are interchangeable because a 5 degree difference in Kelvins is the same as a 5 degree difference in degrees C.)

So that’s thermodynamics, plug-and-play style.  Once you have an answer, it’s good to consider whether your answer is reasonable in units and magnitude.  In this problem, we have a small object that has increased in temperature by a modest number of degrees.  4.81 J is a small amount of energy, so this answer seems reasonable to me. 

Next up: a similar problem that will require more conceptual heavy lifting on our part.

Now it’s your turn:

You decide to cook some pancakes in a cast-iron skillet on your electric stove.  You apply 2000 J of heat to your very heavy (3.31 kg) skillet, which was initially at room temperature (22 degrees C).  If 375 degrees F is the ideal temperature for cooking pancakes, do you need to apply more or less heat to achieve that temperature?  Assume the skillet is pure iron for this problem.

* * *

Bonus fun facts:

Pennies were made of pure copper from 1793 to 1837.  {Source}

375 degrees F as a temperature for cooking pancakes?  Who knows—I always cook pancakes by feel.  But here’s a discussion about griddle temp for pancakes.

LESSON: Human Blood Type and Population Genetics

Today’s lesson is inspired by one of the questions a student asked me earlier this summer.  We’ll be discussing human blood types and population genetics, including how to solve problems on this topic.

The question:

In Capitol City, the allele frequencies of human ABO blood types are as follows:

I^A = 0.2

I^B = 0.3

I^O = 0.5

What is the frequency of type A blood within Capitol City’s population?

There is a lot to know and unpack from this problem.  Let’s start with a quick review of blood types.

Recall that for blood types, A and B refer to the presence of the A and B antigens, respectively, present on red blood cells.  Type A red blood cells express the A antigen; Type B red blood cells express the B antigen.  Type O blood expresses neither A nor B antigen.  That means two genotypes can code for blood that is phenotypically type A:

I^A I^A or I^A I^O

(Why two genotypes?  Because the I^O allele does not code for an antigen.  Instead, the I^O allele contains a mutation that results in a protein that lacks enzymatic activity.)

Similarly, two genotypes can code for blood that is phenotypically type B:

I^B I^B or I^B I^O

Finally, only one genotype can code for blood that is phenotypically type O:

I^O I^O

Now that we’ve established our genotype/phenotype relationships, let’s shift our attention to the second aspect of this question: population genetics.

When you see the words “population genetics,” you should immediately think of this phrase: Hardy-Weinberg equilibrium.  The simplest version of Hardy-Weinberg equilibrium is a population that contains two alleles for a gene.  Let’s say these alleles are A and a, where A is completely dominant to a.  In Hardy-Weinberg terms, A and a are equivalent to p and q, the two alleles in our system.  The Hardy-Weinberg equations (shown below) allow us to move between allele frequencies and genotype frequencies.  We use algebra to do these calculations.

To apply Hardy-Weinberg to our two-allele system, A and a, we would have the following:

pp = AA

pq = Aa

qq = aa  

Let’s apply some numbers here to see how the math works out for a two-allele system.  Let’s say that a population has the following frequencies for the A and a alleles:

A = 0.2

a = 0.8

(Note that it’s entirely possible for a recessive allele to be the most common allele in a population.  Genetic dominance does not imply that it’s the most frequently found allele.)

To calculate the frequency of the three possible genotypes (AA, Aa, and aa), we use the binomial expansion from Hardy-Weinberg:

AA = pp = (0.2)(0.2) = 0.04

Aa = 2pq = 2(0.2)(0.8) = 0.32

aa = qq = (0.8)(0.8) = 0.64

Note that our genotype frequencies should add up to 1, which they do!  Success!

Now, let’s turn our attention back to ABO blood types.  We can’t use our two-allele Hardy-Weinberg equation here because we have three alleles.  Instead, we can modify the equations to include a third allele:

By squaring the trinomial, we now have equations we can use to calculate the frequency of particular genotypes or phenotypes if we have the allele frequencies.

Now let’s solve the original problem in four steps.

Alright, now it’s your turn!  Using the data above for Capitol City, what is the frequency of Type AB blood in that population?

* * *

More resources:

* ABO blood types via Wikipedia (a bit dense but still useful for more information)

LESSON: Mitotic Recombination: Twin Spots

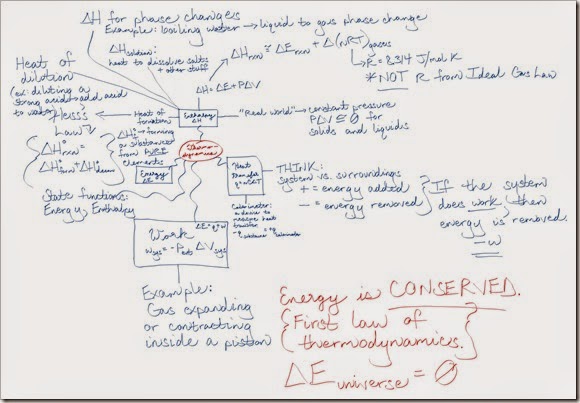
This post will be my first lesson on this site.  I offer these lessons as a gift in the spirit of Sacred Economics by Charles Eisenstein.  If you’ve arrived at this post, I assume you are looking for some help to better understand the classic phenotypes that are seen in studies of mitotic recombination.  In this lesson, I’ll explain the mechanism that may explain one phenotype, twin spots.  Here is a very simple graphic to illustrate the twin spots phenotype:

We can see that we have two “spots” on the fly’s back (dorsal surface for you anatomy fans), right next to each other, and each spot shows a different mutant phenotype (which I’ll explain below).  Note that the wild-type phenotype is a brownish-beige body and straight-ish bristles.

Mitotic recombination is the phenomenon whereby homologous chromosomes swap portions of DNA with each other in non-meiotic cells.  It’s a rare event and often induced either by X-ray radiation or by transgenes that cut and splice DNA when they are expressed.  One of the most interesting questions that can be answered by mitotic recombination is whether a phenotype is cell autonomous.  In other words, is the phenotype of a cell or patch of cells due to the genetic activity within that cell or patch of cells, or does it depend on the genetic activity of a different cell?

In Drosophila, we can study mitotic recombination using mutant alleles that affect the appearance of the body surface.  Dr. Curt Stern did just this using alleles for two genes: yellow (y) and singed (sn)¹.  Homozygous yellow mutants have a yellow body color, while homozygous singed mutants have bent, funky-looking bristles.

(Check it out: yellow mutants and singed mutants.  For the singed mutants, compare D [a wild-type control called Oregon R] to A [a singed mutant].)

Stern worked with female flies that were heterozygous for yellow and singed.  These genes are on homologous chromosomes.  In Stern’s experiment, the mutations were on different but homologous chromosomes.  We can write this genotype like this:

y+ sn- is the genotype of one chromosome, and y- sn+ is the genotype of the other.  Heterozygous mutants like this are also called trans-heterozygotes because the mutations are found on different chromosomes.

Most of the animals Stern examined were wild-type in appearance.  In other words, their body color and bristles did not show mutant phenotypes.  This is what we would expect in animals that have a wild-type copy of each gene.  But sometimes he observed what were dubbed “twin spots” where a spot of yellow was adjacent to a spot of singed bristles.  This cartoon is a nice illustration of the phenotype.  Because of the location of these twin spots, Stern proposed that they were the product of mitotic recombination between the centromere and two loci located on the same side of a chromosome.

So how would that mechanism work?  Let’s draw it out and follow the chromosomes through cell division.

First, let’s consider what the chromosomes look like without mitotic recombination.  For simplicity, I have omitted everything but the most essential details in the diagrams below.  CENT is the centromere of the each chromosome.

Now let’s look at what happens when this parent cell divides in the absence of mitotic recombination.  Here I show the cell before and after it synthesizes new DNA, which results in the replication of the chromosomes.  Note that formally, DNA synthesis is not part of mitosis.  Instead, it is considered part of the cell cycle.

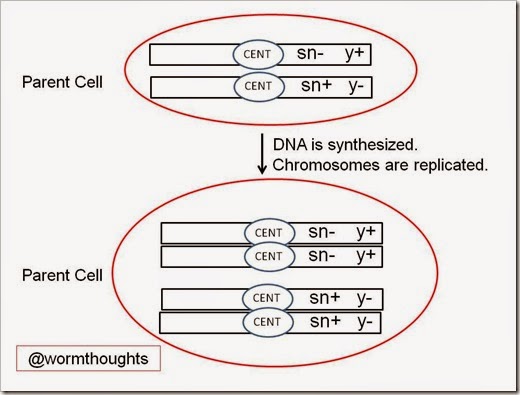
Now that we’ve replicated our homologous chromosomes, let’s follow them through mitosis and cytokinesis.  Note that after the chromosomes have replicated, the sister chromatids are connected via the centromere (CENT in the figure).  This organization will allow sister chromatids to be separated during mitosis and pulled apart into the nuclei of the two daughter cells.  The dotted line below represents cytokinesis, or the dividing of the parent cell’s cytoplasm into two daughter cells.

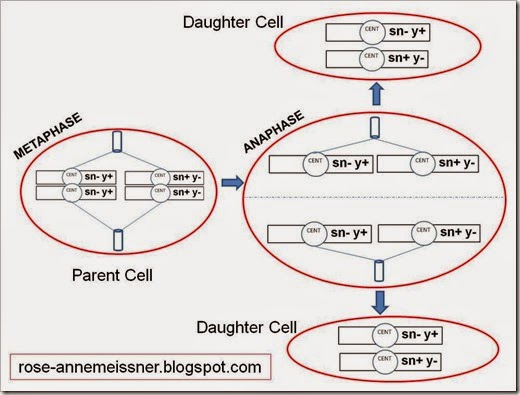
Note that after this cell divides, the daughter cells would have the same genotype (sn- y+/sn+ y-).  Note that all of these cells would show a wild-type phenotype because each cell has a wild-type copy of sn and y.

Now, let’s consider a situation where mitotic recombination occurs.  Scientists aren’t really sure when mitotic recombination happens.  Some think it happens during interphase; that’s what I have shown below (specifically, Gap 2 after DNA synthesis is completed).  The take-home point: mitotic recombination will switch the order of specific sn and y alleles compared to the original parent cell.

First I’ll show the recombination step and the reordered chromosomes.  Note that recombination is taking place between chromosomes 2 and 3.  Also note that the recombination breakpoint is between the centromere and the singed locus.

 

Now we have paired chromatids that have different genotypes.  Chromatids 1 and 2 no longer match, but as you’ll see below, they will segregate during mitosis as though they are genetically identical.  The same thing is true for chromatids 3 and 4.

Let’s follow the chromosomes through mitosis. 

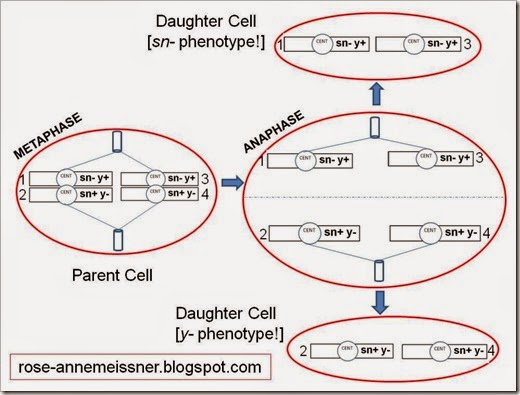
Because of the recombination event that happened during Gap 2, we end up with daughter cells that have different genotypes.  Instead of the sn- y+/sn+ y- genotype that the parent cell has, our daughter cells are as follows:

And finally, here is a cartoon to show how mitotic recombination in a precursor or parent cell could give rise to a twin spot.  The idea here is after the parent cell undergoes mitotic recombination, the new daughter cells replicate themselves and make small populations that we can see visibly as the yellow or singed spots.  (Pardon the reverse orientation on the spots; here I’ve shown the yellow spot on top and the singed spot on the bottom.)

References:

¹Stern, C (1935) The effect of yellow-scute gene deficiency on somatic cells of Drosophila. Proc Natl Acad Sci USA 21: 374-379.  {Find the full-length paper here.} 

For more learning, I like the following links:

* Mosaic Analysis [in Drosophila]

* A good review of what happens to chromosomes during the cell cycle and mitosis 

* * *

Like what you just read?  To connect with me, you can find me on Twitter (I’m @wormthoughts) or by e-mail (r-meissner@u.northwestern.edu).  Or leave a comment below!

Thanks for stopping by!

STUDY TIPS: General Chemistry

I’ve had the pleasure of working with several students in general chemistry this year.  It’s interesting to see chemistry through the eyes of my students.  General chemistry came easily to me as a student; as a tutor, I find myself asking, “When it comes to learning this material, what works?  What doesn’t?  What holes can we fill so that my students have an easier time with the exam?”

Here’s my list of study tips for general chemistry.  What you won’t find here: very basic tips like go to class, pay attention, take notes, work the problem sets.  I assume you know these things.  (But I’ll come back to that point about working the problem sets!)

* You must master the theory and application of chemistry concepts.  What do I mean by this?  Chemistry is a marriage of theoretical ideas, such as equilibrium, and the application of those ideas, such as calculating the equilibrium constant K_eq value if I tell you the concentration of products and reactants in a solution at equilibrium.  A theory question might ask you to predict the direction of a reaction if the reaction quotient Q is less than K_eq.  (Answer: the reaction will keep generating products until Q = K_eq.)  (Pop quiz question: what’s the difference between Q and K_eq?)

Many gen chem exams will mix together theoretical questions and math-based application questions.  You’ll want to be able to answer both.

“What if I don’t have practice questions for theoretical concepts?”  If you are lacking study materials, get in touch with me.  I’ve got a library of chemistry textbooks and practice exams to help you work on mastering gen chem theory.

* You must learn to think in four dimensions: the X, Y, and Z planes and time.  Chemistry takes place across all four of these dimensions.  Students who are, shall we say, spatially challenged (like myself) are going to have to focus their efforts on mastering three-dimensional chemistry.

A simple example from gen chem is molecular geometry: where do electron pairs (lone pairs or the shared pairs of a chemical bond) localize around an atom’s nucleus?  In other words, what is the three-dimensional shape that defines where the electrons are in space?  (Answer: it depends on how many of them we have around an atom.)

The question about time looms large when we start to talk about reaction kinetics.  This topic may be discussed in an abstract way, such as in spontaneous reactions that happen so slowly that they appear to be not spontaneous (such as combustion reactions that require energy, such as a spark, in order to begin), or we might talk specifically about reaction rates and rate constants.

* Work those practice problems, especially the practice exams.  Then practice some more.  It’s not enough to review your notes and think you understand the material.  Practice problems demand that you understand the material and are able to apply it to solve problems.

If I could offer one piece of advice to gen chem students, it would be to focus your study time on practice exams (assuming your instructor provides them to you).  Work as many of the problems as you can.  If you struggle through any problems, go back and work them again.  Try to see the logic that is applied to each problem so that when a similar problem shows up on your real exam, you know how to analyze it.

* Seek out additional learning materials.  I’m going to be really honest here: I dislike a lot of textbooks.  I hated my gen chem textbook in college.  If you find yourself in a similar position, don’t hesitate to seek out additional learning materials.  I’ve been using an awesome chemistry textbook in my tutoring that I can recommend: Chemistry (Third Edition) by Olmsted & Williams.

Also, this is the age of the internet!  There are so many wonderful on-line study materials (including this blog!).  I particularly like ChemWiki and MIT OpenCourseWare on youtube.  (As an aside, as much as I love Wikipedia, I don’t like it as much for studying chemistry.  And that’s okay.  The important thing is to find resources that work for you.)

* Make sure your algebra skills are strong.  A lot of problem-solving in gen chem comes down to setting up the problem as an algebra equation to be solved.  If you feel your algebra skills are weak, you might want to spend some time working on them either before you start gen chem or while you are in the class.  The more you can solve for X, the more comfortable you’ll be with chemistry problems.

* Learn to think about chemistry in terms of units. This tip comes from my partner, Tutor Paul, who has been tutoring engineering students for years.  When solving equations, we want units within a problem to match and cancel out.

One way to test your comfort with units is to do a little free word association.  What unit words come to mind when I say the following?

- energy?

- stoichiometry?

- pressure?

- volume?

- concentration?

For me, I have the following associations:

- energy? Joules.

- stoichiometry? Moles.  Or molar ratios.

- pressure? Atmospheres.

- volume? Liters.

- concentration? Moles per Liter.

My answers are standard units in which amounts are expressed.  A Joule is a unit of energy.  The stoichiometry of a reaction is expressed in moles (or molar ratios).  And so on.  Getting comfortable with gen chem means getting comfortable with units.

* * *

Readers, what else would you add to this list?  Tell me in the comments!

Happy studying!