LESSON: Selection Pressure, Part Two

In this lesson, we’re going to pick up where my last lesson on selection pressure left off.  Here’s the link to the first lesson if you’d like to familiarize yourself with that first.

Today’s lesson focuses on how selection pressure changes allele frequencies over many generations.  Our sample problem is a follow-up to the scenario in my first lesson:

Despite your good work in Capitol City last time, the strange epidemic persisted and all individuals who lack Factor G are now sterile.  Individuals who lack Factor G are genotype gg; individuals who produce Factor G are GG or Gg and have normal levels of fertility.  How many generations will pass until the recessive g allele has a frequency of less than 1%?

In my last lesson, we figured out that when gg individuals cannot reproduce, the frequency of g drops from 0.3 in the parent population to 0.231 in the first generation after selection.  The simple formula for figuring out g’ if gg individuals are not reproducing is g’ = g/(1+g).

Here, g’ refers to the frequency of g in the next generation.  (And if you want to see the derivation of that simple formula, see my last lesson.)

If we do the math, we see that after one generation of selection, g decreased by 23%:

So how do we find the generation at which allele g is less than 1%?

Before we jump to those calculations, let’s consider what these numbers really mean.  After the first round of selection, the frequency of g is 23.1% or 0.231.  This number includes the individuals who are gg, even though they are sterile.  Why is that?  Because when Gg heterozygotes mate, their children will be:

1 GG: 2 Gg: 1 gg

The fact that Gg individuals have normal fertility means that there will be gg children, even though those children are not able to reproduce.

Also, let’s consider the number of Gg heterozygotes in the population after one round of selection pressure.  Again, the frequency of g is 0.231.  The number of Gg hets = 2pq.

2pq = 2(0.769)(0.231) = 0.355 or 35.5%

35% of the population here is Gg, which means that g is being propagated by about a third of the population (a substantial fraction!).

Let’s move on to the calculations to determine when the frequency of g will be less than 1%.

I doubt that you’d be asked to solve a problem like this on an exam without being able to use Excel or a similar program.  The calculations are easy on a spreadsheet but very tedious to do by hand.  I used Excel to solve this problem.  Here’s what my spreadsheet looked like to set up the calculations:

Here are the entries I put into Excel to set up this spreadsheet: 

Cell B1: 0.3 (original value of g before selection)

Cell B6: =B1/(1+B1)

(this is the calculation for g after each round of selection: g’ = g/(1+g))

Cell B7: =B6/(1+B6)

Cells B8-B14: Copy/Paste from cell B7 down to B14.

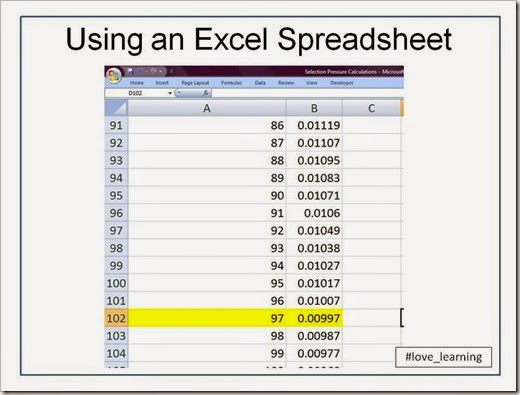
From the image above, you can see that after 9 rounds of selection (Row 14), the frequency of g is 0.081 or 8.1%.  So we’re not done, and we can continue our calculations by copy/pasting Cells A14 and B14 until we reach…

…Cell 102!

We’re looking for the generation at which q drops below 0.01, which happens to occur at the 97th generation of selective pressure.  What’s so interesting to me as a geneticist is that g (or q, in Hardy-Weinberg terms) can persist for so long when gg individuals are sterile.  This example illustrates why recessive deleterious alleles are not easily eliminated from the population.  As long as Gg heterozygotes are healthy, then g will be in the allele pool for a long time.

So that was a lesson on selective pressure and Microsoft Excel techniques.  Got questions, comments, or something else to say?  Tell me in the comments below! 

Thanks for reading!