LESSON: Heat Transfer, Part One

I wrote recently about the importance of algebra in general chemistry.  To illustrate, I’m going to present a lesson in two parts.  This first part is an example of what I call “plug and play” chemistry problems.

I’ve been brushing up on thermodynamics at the gen chem level.  Thermodynamics is a very math-driven branch of chemistry, so it’s a lot of equations and a little bit of theory.  There are at least two conceptual ways to approach problems:

1) Envision the process being described, determine the unknowns, then select the appropriate equation that describes (mathematically) the flow of energy in the system.

2)  Write down the values provides (such as heat capacity and initial temperature) and the value for which you have to solve (such as final temperature), find a formula that contains those terms, then solve for the unknown.

Option #1 is definitely the better choice and the one for which we should strive as we’re learning.  But if I’m honest, I think a lot of us are tempted to use #2 if we can get away with it.  In the second part of this lesson, I’ll show you an example of how option #2 can be insufficient.  Additionally, thermodynamics uses signs (+/-) to indicate the flow of energy into or out of a system.  Because of that, it’s a really good idea to get in the habit of imagining the process so you can double check your math and your signs.  (Or draw it out!  Drawing is always a good idea when studying science.)

(More on drawing later, I think.  It’s a topic worth exploring for science students.)

Let’s consider the following problem and how to find a solution.

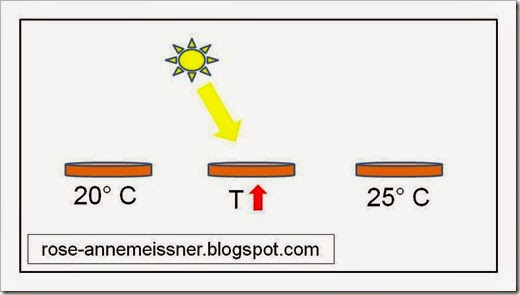
You drop a pure copper penny on the ground while walking to breakfast one day.  The penny’s mass is 2.50 g.  At the time you lost it, the penny’s temperature was 20 degrees C.  When you find it later, the penny is 25 degrees C.  How much energy did the penny absorb from its surroundings between the time you lost it and the time you recovered it?

This problem is pretty simple, but let’s draw a diagram so we can visualize the energy flow.

Heat is flowing into the copper penny from the sun, thus raising the temperature of the copper.

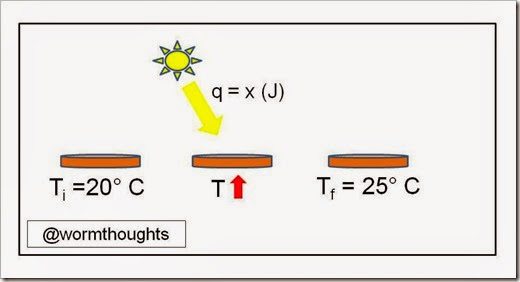
Now let’s apply some technical labels to help us find the right formula.

A quick review of terms:

q = heat flow, usually measured in Joules (J).

T_i = initial temperature (can be degrees C or K)

T_f = final temperature (must have the same units as T_i)

What else do we need to know to solve this problem?  We need to know how easily copper absorbs heat from its surroundings.  This material property is known as heat capacity, and the heat capacity is different for different substances.  The molar heat capacity for copper at 25 degrees C is 24.435 J/mol K.  What does this value mean?  It means that 1 mole of copper requires 24.435 J to raise the temperature 1 K.

(For our purposes, we’ll assume that the heat capacity for copper is the same at 20 degrees C and 25 degrees C.)

Which formula expresses the thermodynamic question asked in this question?

Now that we have a formula to connect heat flow to the change in temperature in a specific substance, we can plug in the values from above and solve the problem.

(Note that in this problem, K and C are interchangeable because a 5 degree difference in Kelvins is the same as a 5 degree difference in degrees C.)

So that’s thermodynamics, plug-and-play style.  Once you have an answer, it’s good to consider whether your answer is reasonable in units and magnitude.  In this problem, we have a small object that has increased in temperature by a modest number of degrees.  4.81 J is a small amount of energy, so this answer seems reasonable to me. 

Next up: a similar problem that will require more conceptual heavy lifting on our part.

Now it’s your turn:

You decide to cook some pancakes in a cast-iron skillet on your electric stove.  You apply 2000 J of heat to your very heavy (3.31 kg) skillet, which was initially at room temperature (22 degrees C).  If 375 degrees F is the ideal temperature for cooking pancakes, do you need to apply more or less heat to achieve that temperature?  Assume the skillet is pure iron for this problem.

* * *

Bonus fun facts:

Pennies were made of pure copper from 1793 to 1837.  {Source}

375 degrees F as a temperature for cooking pancakes?  Who knows—I always cook pancakes by feel.  But here’s a discussion about griddle temp for pancakes.